对比度衰减图是OpticStudio17.5的一个新特性,它提供了一个简单的方法来理解对比度在光学系统中是如何变化或衰减的。在出瞳处将调制传递函数(MTF)的特定频率的对比衰减视为一个分布图。对比度衰减图可以让我们了解到MTF是如何在光瞳处被削弱的。然后,您可以使用这些数据来确定对系统进行哪些更改以改进MTF。在对比度优化过程中同时绘制了对比度衰减,这是OpticStudio17中引入的一种新功能,它使用摩尔-埃利奥特(Moore-Elliott)方法对MTF进行优化,至少比传统方法快30倍。
如何利用瞳孔函数的自相关来计算MTF的原理,有助于解释对比度衰减。在这里没有描述推导过程。
对于一个光学系统中指定的视场和波长,你可以通过一个复杂的瞳函数P(x,y)追迹来确定物方到图像的光线,然后追迹这些光线到出瞳。
这个复杂的瞳函数可以被描述为
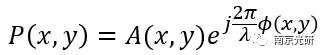
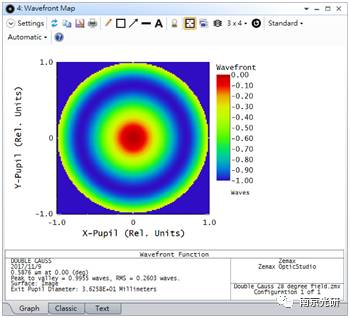
A(x,y)是振幅,λ是波长,ϕ(x,y)是射线的光程差,计算的是在出瞳处主光线的光程差。相位部分ϕ(x,y)被称为波阵面。要想在OpticStudio中看到波阵面,可以在波前导图中进行分析。
对于一个特定的场和波长,MTF可以通过使用P(x,y)的自相关的模量来计算,它被ξx=ξy=0,所规一化,ξx和ξy分别是x和y方向的空间频率。
也就是说,MTF可以被描述为空间频率的函数
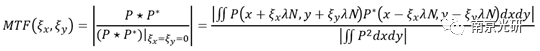
P*是P的复共轭,λ是波长,N是工作的F数,也可以写成F/#。
因为MTF是一个二维频域分布,你可以在一个特定的频率,计算MTF。ξt是在x–或y-方向上先转移2ξtλN,的光瞳处空间频率函数,计算其复数的共轭,乘以未移位的光瞳函数转移和未移位光瞳函数重叠区域进行积分,然后计算其模量。
为简单起见,您可以将移位次数为2ξtλN:
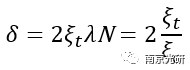
ξc是截止频率
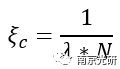
下面的图显示了瞳孔在x-方向上的移动δ。
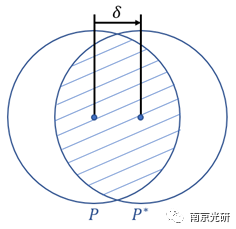
对于给定的δ,注意,当ξt=ξc时,δ=2。这个条件对应于一个Pupil的移位,等于标准化的pupil直径。也就是说,P和P*的边是重合的,但是P和P*没有重叠,导致MTF等于零。要了解更多关于标准化pupil直径的信息,请参阅OpticStudio帮助文件中的NormalizedPupilCoordinates。
当定义参数Grid=0时,自相关方法也用于计算MTF值,该值用于函数操作数MTFT、MTFS和MTFA。
相位差和对比度衰减的关系
考虑到MTF被计算为pupil函数的自相关,从未移动的pupilP和移位的pupilP*的两者重叠点等于未移位PupilP乘上δ。
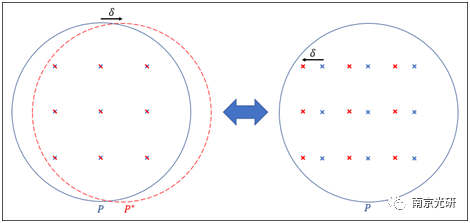
当一个复数A1乘以另一个复数A2共轭时,它的大小与相差的余弦成正比
因此,为了使一个特定频率的MTF最大化,任何来自同一视场和Pupil上位移δ的两束光线的相位差(ϕ1-ϕ2)应该为零或者是2π.的倍数。因此,当使用对比优化优化系统时,OpticStudio尝试将采样射线对的相位差最小化。
虽然在优化MTF时,相位差被最小化,但正是由于相位差异导致了对比度的变化。摩尔-埃利奥特方法使用了相差的余弦值来计算pupil中每个采样点的对比衰减,如下所述
ϕ1和ϕ2是同一场的两束射线的相位。当计算sagittal对比衰减时,这两束光在Px方向上被分离位移δ。当计算切向的对比损失时,这两束光被Py方向分开δ。
对比对衰减图
对比损失图可以直观地看到相位差和对比度衰减,可以用来分析和改进光学系统。如下图所示,对比损失图显示了Pupil的每个采样点的对比度衰减和波前信息,分别由一个圆圈和小指示线表示。
在OpticStudio中查看,Analyze>Wavefront>ContrastLossMaporAnalyze>MTF>ContrastLossMap.。
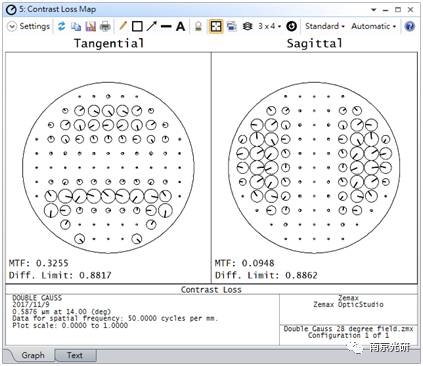
每个圆圈的大小代表了pupil中那个位置的对比度衰减的大小。当对比度衰减为1时,圆圈的大小为最大,当对比损失为0时,圆圈的大小为最小值。
指针的方向表示波前信息。对于pupil的每一点,计算了移位和未移位的pupil函数的平均光程差(OPD),乘上2π。这个值决定了指针的方向,如下图所示。当OPD为0时,指示器指向+X方向,并逆时针方向旋转,就像一般的OPD增加一样。
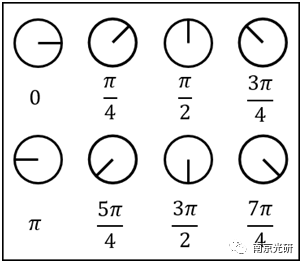
Interpretation(示例描述)
对比度衰减图显示的是一个特定的视场和波长,在pupil的坐标中,对比度小于1,因此MTF比衍射极限MTF要小。
考虑如下图所示的一个5度视场的胶合透镜。针对20线对的对比度优化胶合镜的镜片曲率。
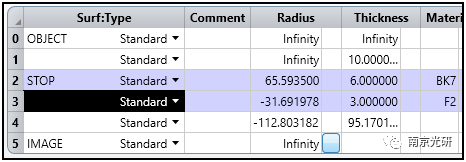
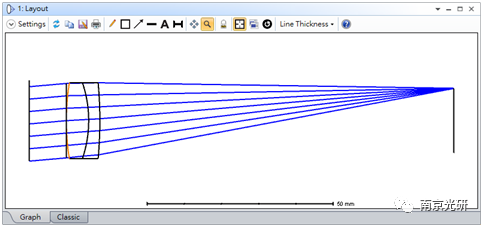
下图给出了MTF图和20线对处的对比度衰减图
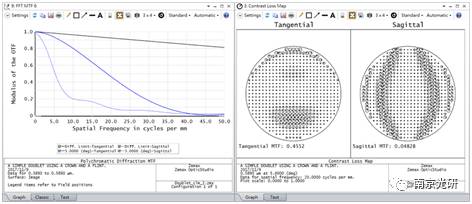
为了增加切向的MTF,我们可以将胶合镜的第一个面变为非球面,然后通过加入一个单一的非球面系数作为一个变量来优化这个新系统。下面的图显示了在优化期间使用每个系数顺序时产生的MTF。黑色曲线显示了衍射极限MTF。
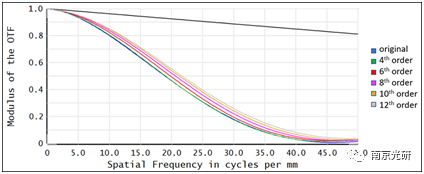
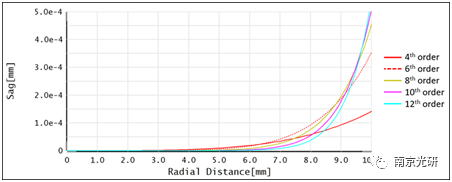
结果表明,MTF在每种情况下都略有改进。为了理解这是为什么,你可以分析每一个结果表面的sag的影响。在这种情况下,使用单个系数进行优化只会显著地改变镜头边缘的表面sag。如下图所示,第12个非球面系数在非球面的边缘上对sag的影响最大。第12个非球面系数也会导致最高的MTF。
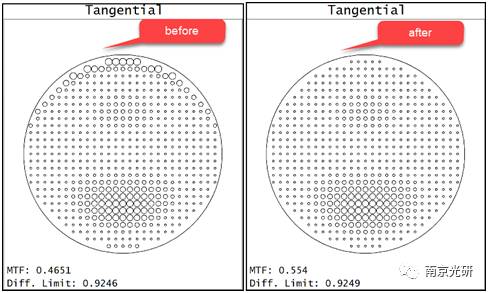
如下图所示,在对12项非球面系数进行优化前后比较对比度衰减图,可以清楚地看出,pupil边缘的对比度衰减消除了,这对MTF的影响很小。然而,表面边缘的变化对切向对比度衰减没有明显的影响。
因此,你可以假设,为了消除切向对比衰减的影响,你需要优化至少两个非球面系数,因为一个系数单独不能充分地控制在中心和边缘之间的形状。如下图所示,当系数同时优化时,MTF对各种系数组合的改进要显著得多。
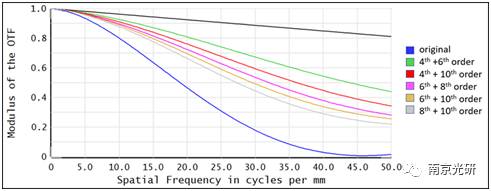
此外,当使用4-6阶系数分析优化结果的对比度衰减图和sag贡献时,你会发现凸块大大减少了。
当从第4和第6个非球面系数来检查sag的贡献时,你会注意到SAG的变化主要是在孔的中心和边缘之间的区域。在优化之前,这些变化与切向对比度衰减图的凸起有相似的位置,如下图所示。
这个例子演示了如何使用OpticStudio17.5的对比度衰减图显示出表面形状或改变的表面形状,可以帮助优化在特定的空间频率上的MTF。
Shearinginterferogram(剪切干涉图)
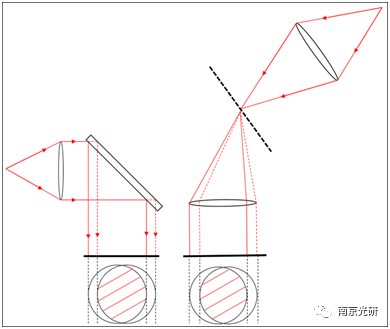
由于对比度衰减是基于相位差异的余弦值,当它被用于高采样时,对比度衰减图可以模拟剪切干涉图。剪切干涉计将一束光线分成两束,并将产生的光束以相同的方向传播,但侧向位置有轻微偏移的。下面的图片展示了两个示例图。
左边的示意图演示了使用平板玻璃板分割测试光束;右边的示意图演示了使用衍射光栅对测试光束进行分裂。剪切干涉图是两光束在探测器上的干涉图样。
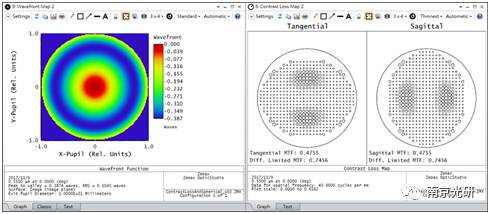
有关剪切干涉计的更多信息,请参阅维基百科的文章“Shearinginterferometer”。因为对比度衰减图在计算中使用了pupil的一个偏移量,所以可以将其结果与真实的剪切干涉图测量联系起来。例如,在以下系统中,波前导图显示了明显的球差。同一系统的对比度衰减图显示了一个典型的剪切干涉图,它包含了球差。
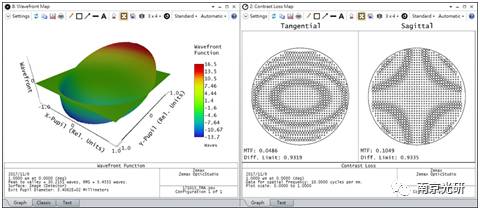
同样的情况也适用于以下显示慧差的波前图;这张对比度衰减图显示的是一种包含慧差的剪切干涉图。
总结:
对比度衰减图提供了一种简单的方法来理解对比度在光学系统中是如何变化的。它将MTF的一个特定频率与在出瞳中进行对比,并采用与摩尔-埃利奥特方法进行对比优化时使用的相同计算方法。正如所演示的,对比度衰减映射可以用来推断改进系统性能所需要的变化。由于对比损耗图使用的是光的相位差和移位的瞳孔,它也可以用来模拟剪切干涉图,并识别光学系统中的特殊畸变。
关注南京光研
